Calibration of gamma
Shown below is the transformation technique applied to the concentration and current equations to determine u*c and the Rouse parameter a1. Also shown is a representative concentration and current profile.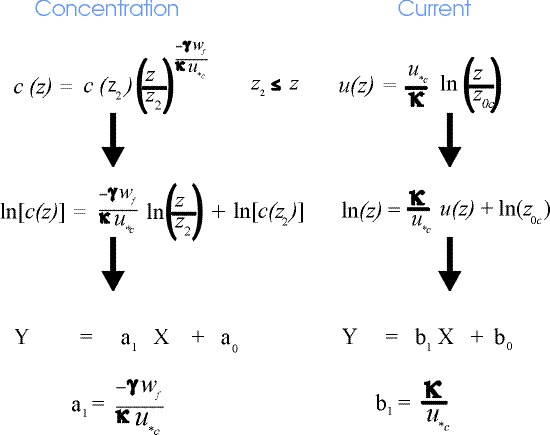
Once a1 and b1 are calculated from the profile data, linear statistics are used to produce the regression coefficient (R) to determine the quality of the the best fit.
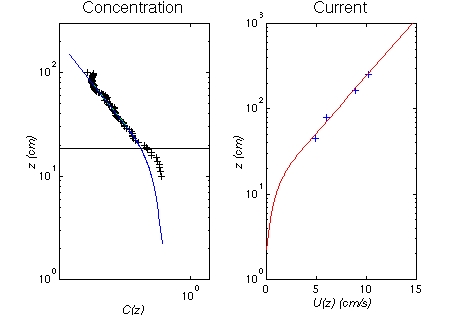
To determine a cutoff for R, we use the Z = atanh(R) statistic adopted by Gross et al. (1992). This provides an objective cutoff since Z has a normal distribution barring any process (bio-fouling, low flow) that may alter the current profile from the logarithmic variation with height expected in the constant stress layer. The Z statistic for the 1995 data is shown below for the full data set (left) and for data up to year day 250 (right), when bio-fouling was suspected to begin to significantly compromise data quality.
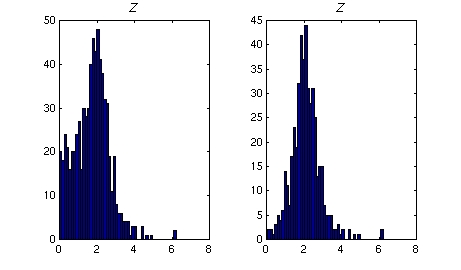
Inverting the mean of Z set the minimum R2 for the current and concentration at 0.94 and 0.87, respectively. Using only bursts that were greater than the cutoff, produced an average gamma of 0.41. This is lower than the widely reported value 0.74, and suggests that gamma may be grain size dependent with larger grains producing smaller gamma. Similar claims have been made in the past (Villaret and Trowbridge 1991; Hill et al. 1988).